Aufgaben
Aufgabe 1
Berechne die fehlende Größe des Dreiecks.
| a) | b) | c) | |
|---|---|---|---|
| Grundseite g | 3 cm | 8cm | |
| Höhe h | 6 cm | 30 cm | |
| Flächeninhalt A | 24 cm² | 12 cm² |
Die fehlende Größe des Dreiecks lautet:
| a) | b) | c) | |
|---|---|---|---|
| Grundseite g | 3 cm | 1,6cm | 8cm |
| Höhe h | 6 cm | 30 cm | 3cm |
| Flächeninhalt A | 9 cm² | 24 cm² | 12 cm² |
Rechnungen:
\[\begin{align} a) \quad\quad A &= {1 \over 2} \cdot g \cdot h \\ {}\\ A &= {1 \over 2} \cdot 3 cm \cdot 6 cm \\ {}\\ A&= 9 cm² \quad \end{align}\]
\[\begin{align} b) \quad\quad A\quad &= {1 \over 2} \cdot g \cdot h \\ {}\\ 24 cm² &= {1 \over 2} \cdot g \cdot 30cm \\ {}\\ 24 cm² &= {1 \over 2} \cdot 30cm \cdot g \\ {}\\ 24 cm² &= 15cm \cdot g \quad\quad | : 15 cm\\ {}\\ {8 \over 5} cm &= g\\ {}\\ \Rightarrow g &= 1,6 cm \end{align}\]
\[ \begin{align} c) \quad\quad A\quad &= {1 \over 2} \cdot g \cdot h \\ {}\\ 12 cm² &= {1 \over 2} \cdot 8cm \cdot h\\ {}\\ 12 cm² &= 4cm \cdot h \quad |:4cm\\ {}\\ 3cm &= h \end{align}\]
Aufgabe 2
Gegeben ist ein Dreieck mit Grundseite \(g\) und Höhe \(h\). Wie verändert sich der Flächeninhalt, wenn die Höhe verdoppelt/vervierfacht/halbiert wird?
Betrachte zunächst folgende Animation:
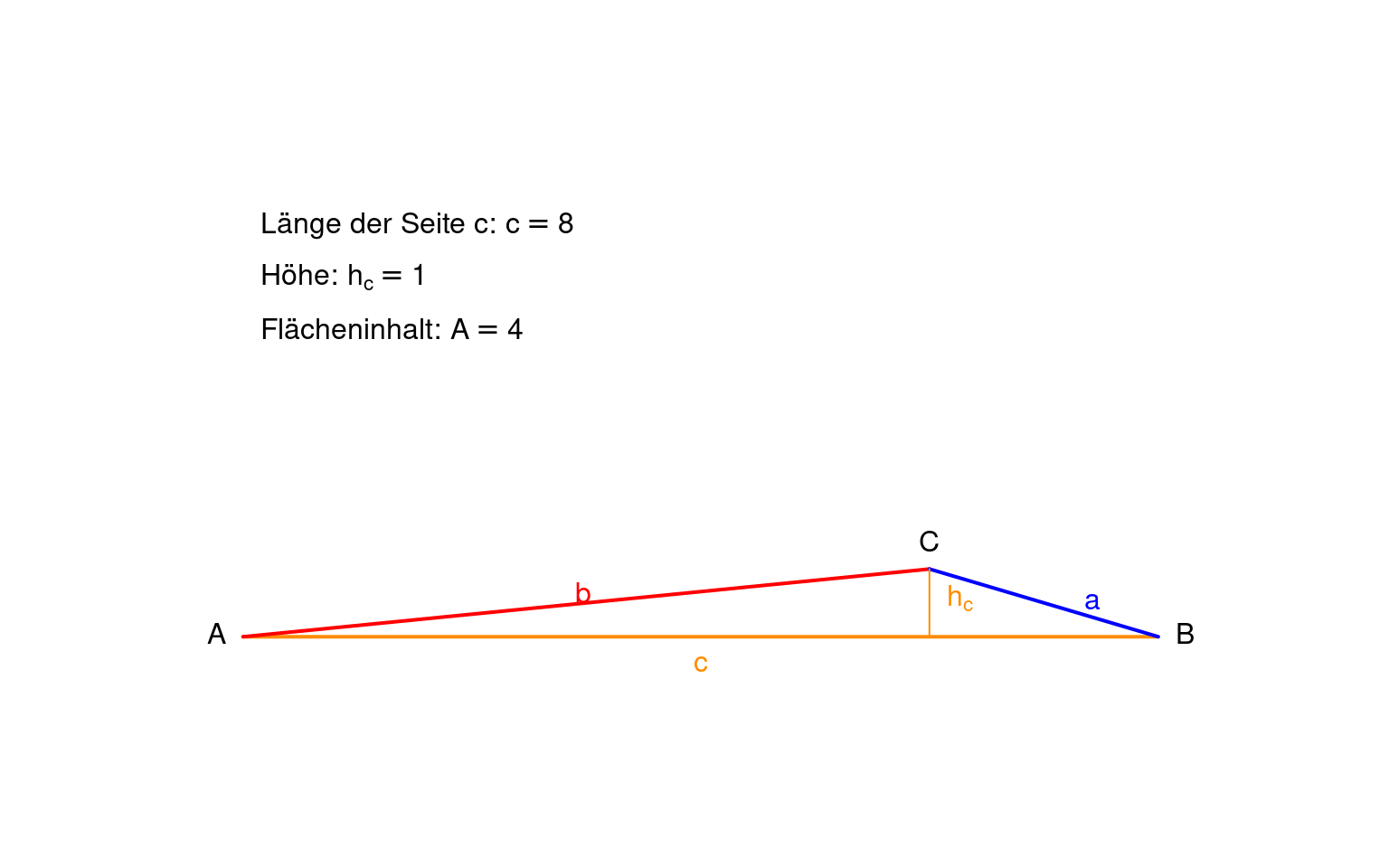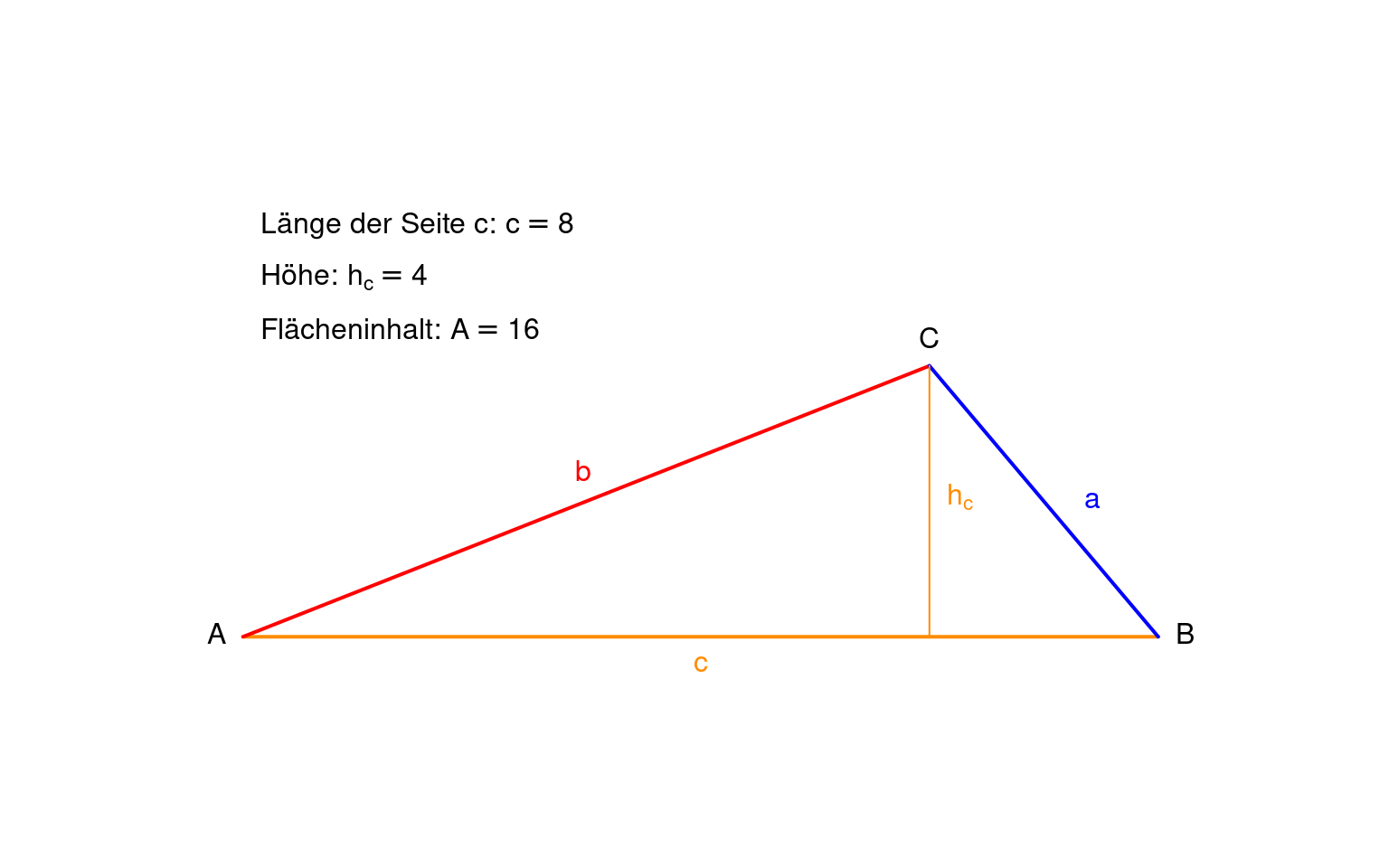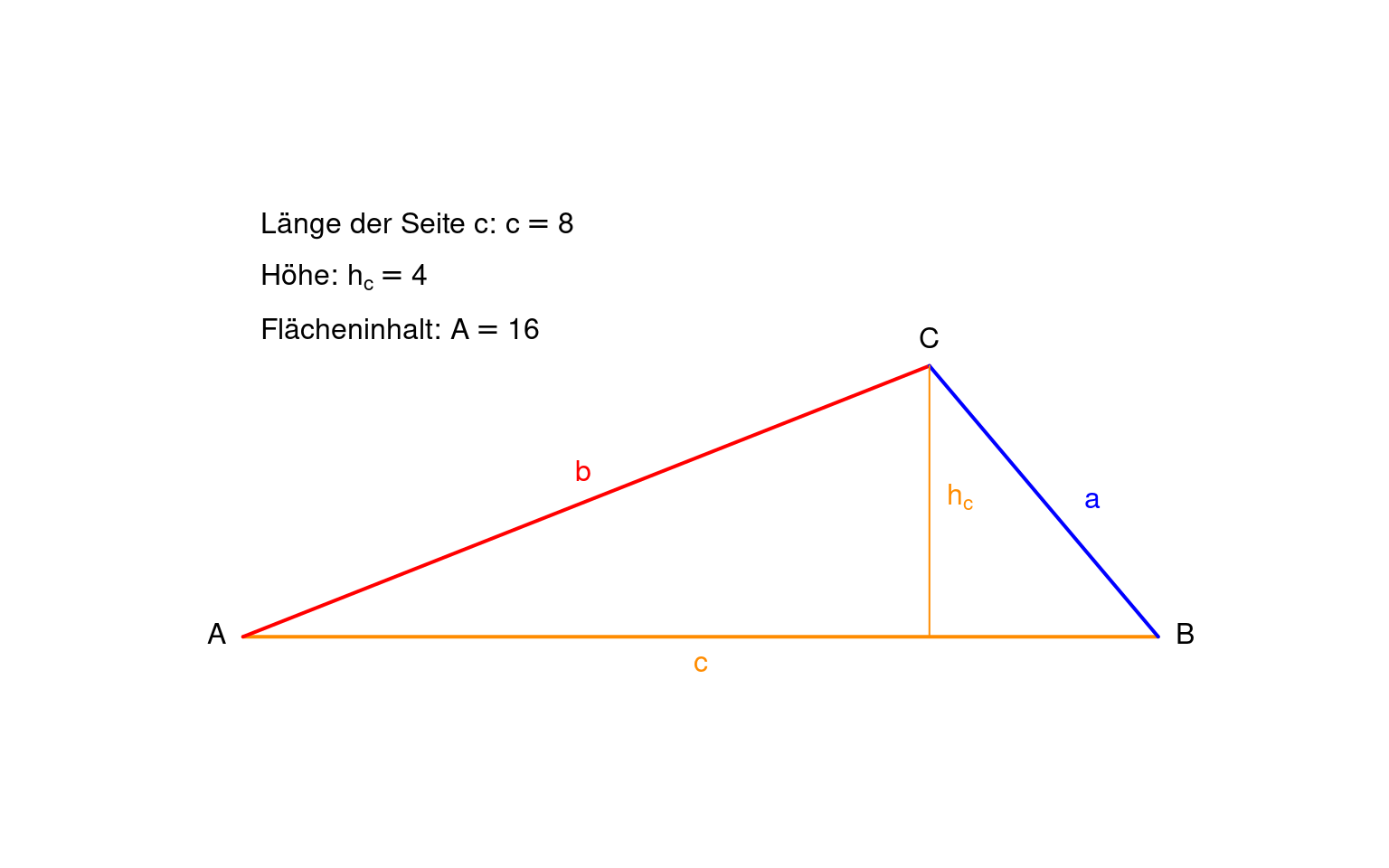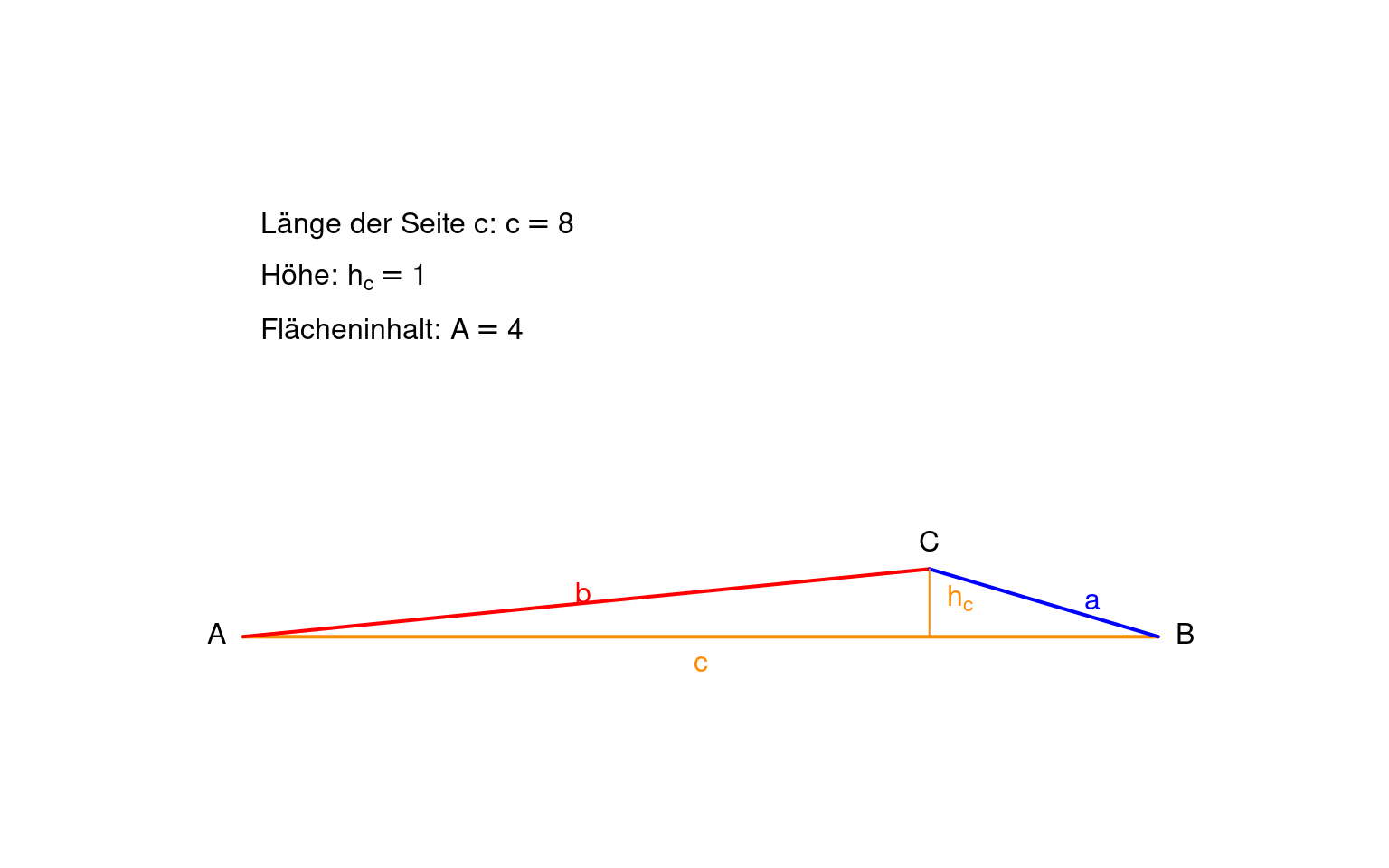
Notiere deine Beobachtungen:
Wenn die Höhe verdoppelt wird, …… sich der Flächeninhalt.
Wenn die Höhe vervierfacht wird, …. sich der Flächeninhalt.
Wenn die Höhe halbiert wird, … sich der Flächeninhalt.
Versuche nun deine Beobachtungen auch zu zeigen. Verändere dafür die Variablen in der Gleichung zur Berechnung des Flächeninhaltes eines Dreiecks auf geeignete Weise.
- Folgende Beobachtungen lassen sich hier notieren:
- Wenn die Höhe verdoppelt wird, verdoppelt sich der Flächeninhalt.
- Wenn die Höhe vervierfacht wird, vervierfacht sich der Flächeninhalt.
- Wenn die Höhe halbiert wird, halbiert sich der Flächeninhalt.
Beweis: Den Flächeninhalt eines Dreiecks berechnet man folgendermaßen: \[ A = {1 \over 2} \cdot g \cdot h \] Verdoppelt man die Höhe \(h\), so erhält man eine neue Höhe der Länge \(2h\), für die Berechnung des Flächeninhaltes \(A_{neu}\) des neuen Dreiecks mit der verdoppelten Höhe ergibt sich dann: \[\begin{align} A_{neu} &= {1 \over 2} \cdot g \cdot (2h) = \\ &= 2 \cdot \underbrace{\left({1 \over 2} \cdot g \cdot h\right)}_{=A} = 2 \cdot A \end{align}\] Damit ist der neue Flächeninhalt, der zur verdoppelten Höhe gehört, doppelt (zweimal) so groß wie der alte Flächeninhalt.
Die beiden anderen Aussagen zeigt man genauso! Versuch’s doch auch mal mit der vierfachen Höhe!
Aufgabe 3
In einem Dreieck beträgt der Flächeninhalt \(A=20cm²\). Die Höhe \(h_c\) ist doppelt so lang wie die zugehörige Grundseite \(c\). Berechne \(c\) und \(h_c\).
Gegeben
Gegeben ist also:
- Der Flächeninhalt: \(A=20cm²\) und
- der Hinweis, dass die Höhe \(h_c\) doppelt so lang ist wie die zugehörige Grundseite \(c\), also: \(h_c= 2 \cdot c\).
Den Flächeninhalt eines Dreiecks berechnet man folgendermaßen: \[ A = {1 \over 2} \cdot c \cdot h_c \]
Einsetzen
Setzt man nun alle Angaben ein, erhält man folgenden Gleichung:
\[ 20 cm² = {1 \over 2} \cdot c \cdot (2c) \]
Auflösen
Diese Gleichung muss man jetzt nach \(c\) auflösen:
\[ \begin{align} 20 cm² &= {1 \over 2} \cdot c \cdot (2c) \\ {}\\ 20 cm² &= {1 \over 2} \cdot 2 \cdot c \cdot c \\ {}\\ 20 cm² &= c² \quad\quad\quad |\sqrt{\quad}\\ {}\\ \Rightarrow c &= \sqrt{20} cm \approx 4,47 cm \\ \Rightarrow h_c &= 2 \cdot c = 2 \cdot \sqrt{20} cm \approx 8,94cm \end{align}\]
Antwort
Die Seite \(c\) ist also ungefähr 4,47 cm lang und die Höhe \(h_c\) hat eine Länge von etwa 8,94 cm.
Aufgabe 4
Berechne den Flächeninhalt des Dreiecks. Wähle dafür passende Größen aus.
| a) | b) | c) | |
|---|---|---|---|
| gegebene Seiten | \(a=5cm\), \(b=4cm\) | \(b=8m\), \(c=6m\) | \(b=4cm\), \(c=5cm\) |
| gegebene Höhen | \(h_a = 2,4 cm\), \(h_b = 3cm\) | \(h_b =3,75m\), \(h_c =5m\) | \(h_a =2cm\), \(h_b = 3,1 cm\) |
a)
Für die Berechnung des Flächeninhaltes des Dreiecks wähle ich die Seite \(b=4cm\) und die zugehörige Höhe \(h_b = 3cm\), da die Rechnung mit diesen Angaben ein bisschen einfacher ist.
Rechnung: \[ \begin{align} A &= {1 \over 2} \cdot g \cdot h \\ {}\\ & = {1 \over 2} \cdot 4 cm \cdot 3cm \\ {}\\ & = 6 cm² \end{align}\]
b)
Für die Berechnung des Flächeninhaltes des Dreiecks wähle ich die Seite \(c=6m\) und die zugehörige Höhe \(h_c = 5m\), da die Rechnung mit diesen Angaben ein bisschen einfacher ist.
Rechnung: \[ \begin{align} A &= {1 \over 2} \cdot g \cdot h \\ {}\\ & = {1 \over 2} \cdot 6m \cdot 5m \\ {}\\ & = 15m² \end{align}\]
c)
Für die Berechnung des Flächeninhaltes des Dreiecks wähle ich die Seite \(b=4cm\) und die zugehörige Höhe \(h_b = 3,1 cm\). Zur Seite \(c\) fehlt die Angabe der zugehörigen Höhe \(h_c\), ebenso wie zur Höhe \(h_a\) die Angabe der zugehörigen Seite \(a\) fehlt.
Rechnung: \[ \begin{align} A & = {1 \over 2} \cdot g \cdot h \\ {}\\ & = {1 \over 2} \cdot 4cm \cdot 3,1cm \\ {}\\ & = 6,2 cm²\end{align} \]
Aufgabe 5 - Zusatzaufgabe
Im folgenden mathematischen “Versuchsaufbau” kannst du mit einem Dreieck experimentieren. Ziehe an den Ecken. Verschiebe sie. Beobachte, wie sich die Höhen verhalten. Wirf auch einen Blick auf die Formeln zur Berechnung des Flächeninhaltes.
Verändere das Dreieck so, dass eine Höhe außerhalb des Dreiecks liegt. Schaffst du es, dass nur eine Höhe außerhalb des Dreiecks liegt?
Verändere das Dreieck so, dass eine Höhe genau auf einer Dreiecksseite liegt. Schaffst du es, dass nur eine Höhe auf einer Dreiecksseite liegt? Welches besondere Dreieck entsteht, wenn eine Höhe mit einer Dreiecksseite übereinstimmt? Was fällt dir in diesem Fall bei den Formeln zur Berechnung des Flächeninhaltes auf?
Konstruiere drei unterschiedliche Dreiecke mit dem Flächeninhalt 100.
Aufgabe 6 - Zusatzaufgabe
Berechne die fehlende Größe des Dreiecks.
| a) | b) | c) | d) | e) | f) | |
|---|---|---|---|---|---|---|
| Grundseite g | \(6 cm\) | \(4 m\) | \({1 \over 2}cm\) | \(3,2 km\) | ||
| Höhe h | \(8400 m\) | \(8cm\) | \(125cm\) | |||
| Flächeninhalt A | \(12,6 cm^2\) | \(32 m^2\) | \(10,08 km^2\) | \(8,64 km^2\) | \(2 m^2\) |
Aufgabe 7 - Zusatzaufgabe
Zeichne das Dreieck in ein Koordinatensystem und ermittle den Flächeninhalt. Wähle als Achseneinteilung 2 Kästchen = 1 Einheit.
A(3|0); B(8|0); C(6|5)
A(9|1); B(9|9); C(5|5)
Aufgabe 8 - Zusatzaufgabe
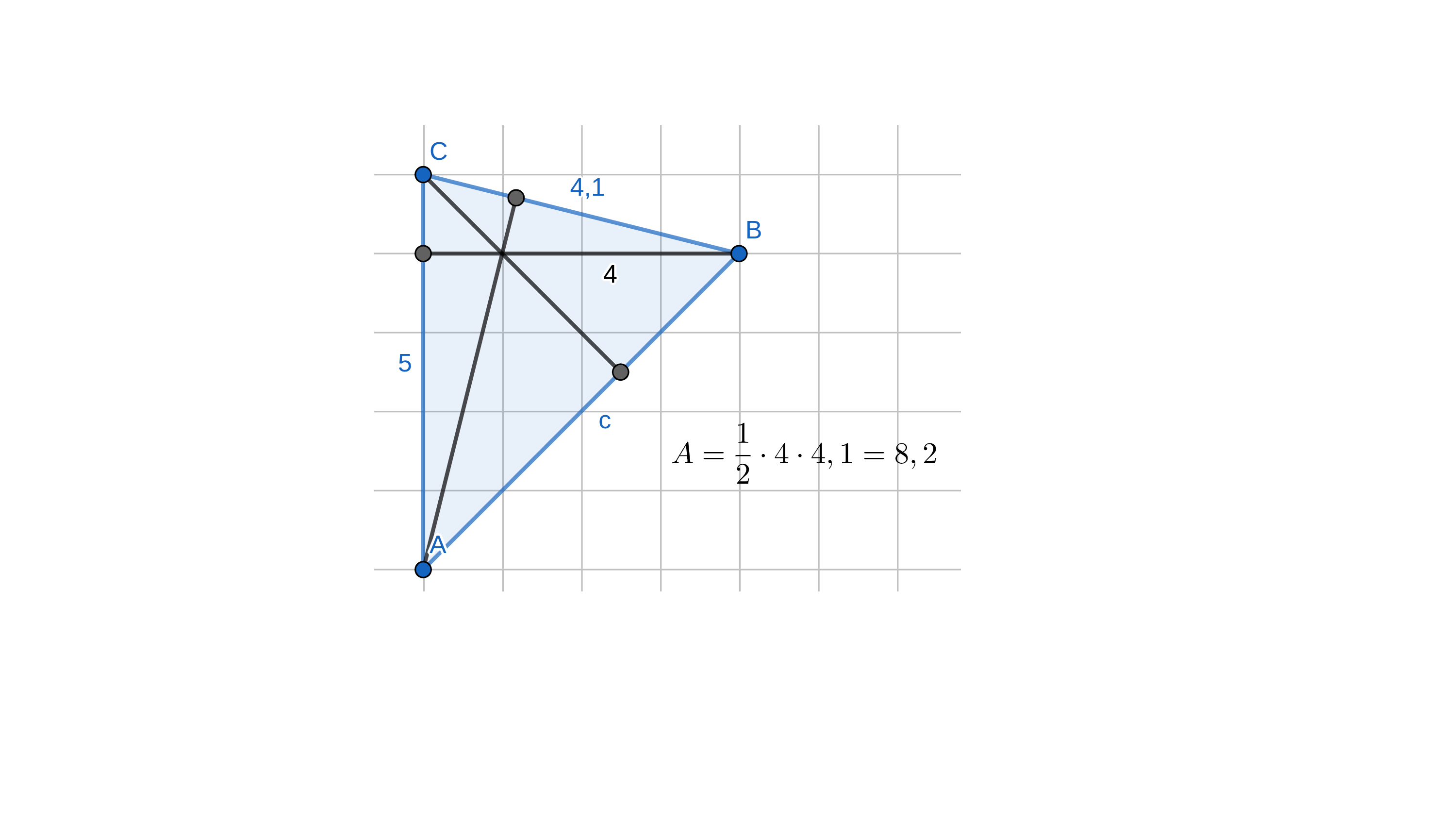
Erkläre und korrigiere den Fehler.