3.1 Mehrstufige Zufallsexperimente

Mehrstufige Zufallsexperimente sind Zufallsexperimente, die aus mehreren nacheinander ausgeführten Versuchen bestehen. Ihre Ergebnisse sind zusammengesetzte Ergebnisse.

Beispiele sind:

• das zweimalige (dreimalige, viermalige, …) Würfeln mit einem Würfel. Beim zweimaligen Würfeln könnte das zusammengesetzte Ergebnis z.B. lauten “erst 3, dann 5”.

• genauso kann natürlich auch das gleichzeitige Würfeln mit zwei (drei, vier, …) unterscheidbaren Würfeln interpretiert werden. Beim gleichzeitigen Würfeln mit einem blauen und einem roten Würfel etwa kann das zusammengesetzte Ergebnis lauten “blau 3, rot 5”.

• das zweimalige (dreimalige, viermalige,…) Werfen einer Münze. Beim zweimaligen Werfen einer Münze könnte das zusammengesetzte Ergebnis z.B. lauten " erst Zahl, dann Kopf". Analog zum Würfel kann auch hier das gleichzeitige Werfen unterscheidbarer Münzen genauso interpretiert werden.

• mehrere Lose nacheinander aus einer Lostrommel ziehen.

Besonders übersichtlich lassen sich mehrstufige Zufallsexperimente in einem Baumdiagramm darstellen. So kann man beispielsweise das zweifache Werfen einer Münze durch das folgende Baumdiagramm darstellen:

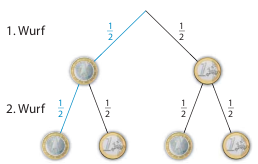
Dabei ist es egal, ob man eine Münze zweimal wirft oder aber zwei Münzen gleichzeitig wirft. Im ersten Fall entspricht die erste Stufe dem ersten Münzwurf und die zweite Stufe dem zweiten Münzwurf. Im zweiten Fall entspricht die erste Stufe eben dem Wurf der einen und die zweite Stufe dem Wurf der anderen Münze.

In beiden Fällen hilft der Baum eine übersichtliche Darstellung der möglichen Ergebnisse zu erhalten. Diese kann man nun alle an den Pfadenden ablesen: \(\Omega=\{KK,\; KZ,\; ZK,\; ZZ\}\), wobei K für Kopf (hier eigentlich eher Adler) und Z für Zahl steht. Gleichzeitig weiß man also auch, wie viele Ergebnisse möglich sind: 4.