2.3 Wahrscheinlichkeit - da war doch was
Bevor der Begriff der Wahrscheinlichkeit eingeführt wird, beschäftigen wir uns mit den Grundbausteinen der Wahrscheinlichkeitsrechnung, den sogenannten zufälligen Ereignissen.
Zufallsexperimente
Bei der Durchführung vieler Experimente kann eines von mehreren möglichen Ergebnissen eintreten. Dabei sind zwar die verschiedenen Ergebnisse, die eintreten können bekannt, vor der Durchführung des Experiments weiß man jedoch nicht, welches Ergebnis tatsächlich eintreten wird. In solchen Fällen sagt man, das Ergebnis hängt vom Zufall ab. Deshalb nennt man derartige Experimente auch Zufallsexperimente.
Ein Zufallsexperiment liegt vor, wenn folgende vier Bedingungen erfüllt sind:
Ein Zufallsexperiment kann verschieden ausgehen.
Alle möglichen Ausgänge oder auch Ergebnisse des Experiments können vor dem Experiment angegeben werden.
Wie das Experiment ausgehen wird, lässt sich nicht mit Sicherheit voraussagen.
Das Experiment kann unter gleichen Bedingungen beliebig oft wiederholt werden.
Beispiele für Zufallsexperimente sind:
Würfeln, eine Münze werfen, Lotto spielen, einen Gegenstand blind aus einem Sack ziehen, die Körpergröße, das Gewicht oder auch den Blutdruck einer zufällig ausgewählten Person messen usw..
Aufgabe 1
Ein Zufallsexperiment ist ein Vorgang, dessen man nicht kann. Bei einem sollen Ausgänge möglich sein und es soll unter den Bedingungen wiederholbar sein.
Eine Münze oder zählen zu Zufallsexperimenten. ist kein Zufallsexperiment, da kein Zufall im Spiel ist.
Aufgabe 2
Entscheide, ob es sich um ein Zufallsexperiment handelt.
Lose ziehen
Würfeln
Die Temperatur bestimmen, bei der Eis schmilzt
Blind eine Spielkarte aus einem Kartendeck ziehen
Die Innenwinkelsumme eines zufälligen Dreiecks bestimmen
Die Ergebnismenge eines einfachen Zufallsexperiments
Die möglichen Ausgänge eines Zufallsexperiments werden als Ergebnisse bezeichnet. Die Menge der möglichen Ausgänge bezeichnet man als Ergebnismenge. Sie fasst alle Ausgänge eines Zufallexperiments zusammen.
Schreibweise:
Sprich: “Die Ergebnismenge Omega besteht aus den Ergebnissen a, b und c.”
Beispiele:
Eine Münze werfen hat die Ergebnismenge:
Würfeln hat die Ergebnismenge:
An dem unten abgebildeten Glücksrad drehen hat die Ergebnismenge:
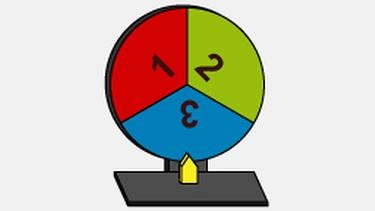
Aufgabe 1
Notiere die Ergebnismengen für folgende Zufallsexperimente:
- Würfeln mit folgenden Würfeln


- Man dreht folgende Glücksräder

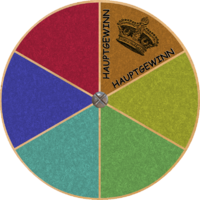
- Man würfelt zwei “normale” Würfel und bildet anschließend die Augensumme.
- Würfel mit acht Seiten:
Würfel mit zwanzig Seiten:
- Erstes Glücksrad:
Zweites Glücksrad:
- Die Augensumme bei einem Wurf mit zwei Würfeln:
Aufgabe 2
Beschreibe passende Zufallsexperimente für folgende Ergebnismengen.
Man dreht ein Glücksrad, das vier Sektoren mit den Farben weiß, schwarz, rot und blau hat.
Man zieht ein Los aus einer Lostrommel, die Nieten, kleine, mittlere und große Gewinne enthält.
Man wählt “zufällige Wiedergabe” bei einer Playliste, die nur vier Songs enthält.
Zufällige Ereignisse
Ein zufälliges Ereignis (oder einfach Ereignis) ist eine Teilmenge der Ergebnismenge. Ein Ereignis ist also ein möglicher Versuchsausgang eines Zufallsexperiments, der aus einem oder mehreren Ergebnissen besteht.
Mit anderen Worten: Mehrere Ergebnisse können zu einem Ereignis zusammengefasst werden.
Schreibweise:
Beispiele:
- Das Würfeln einer geraden Zahl kann geschrieben werden als
- Das Würfeln einer Zahl kleiner 3 kann geschrieben werden als
Es gibt drei besondere Ereignisse:
Das Elementarereignis: Es enthält nur ein Ergebnis. [Eine 1 würfeln oder “Kopf” werfen.]
Das sichere Ereignis: Es enthält alle möglichen Ergebnisse und tritt daher bei jeder Durchführung des Zufallsexperiments ein. [Eine 1, 2, 3, 4, 5 oder 6 würfeln. “Kopf” oder “Zahl” werfen.]
- Das unmögliche Ereignis: Es enthält kein Ergebnis. [Eine 8 würfeln oder “Rand” werfen.]
Aufgabe 1
Du hast folgende Urne. In ihr sind verschieden farbige, nummerierte Kugeln.

Als Zufallsexperiment zieht man nun eine Kugel aus der Urne. Formuliere Ereignisse, die folgende Eigenschaften erfüllen.
- Die Ereignismenge umfasst 3 Ergebnisse.
Ereignis: Die Zahl auf der gezogenen Kugel ist durch 3 teilbar. Ereignismenge:
- Die Ereignismenge umfasst kein Ergebnis.
Ereignis: Es wird eine weiße Kugel gezogen. Ereignismenge:
- Die Ereignismenge umfasst 4 Ergebnisse.
Ereignis: Es wird eine Kugel gezogen, auf der eine Zahl steht, die kleiner ist als 5. Ereignismenge:
- Die Ereignismenge umfasst ein Ergebnis.
Ereignis: Die gelbe Kugel wird gezogen. Ereignismenge:
- Die Ereignismenge umfasst 6 Ergebnisse.
Ereignis: Es wird eine Kugel gezogen, auf der eine Zahl zwischen 1 und 6 steht. Ereignismenge:
Aufgabe 2
Schreibe die Ereignismengen zu folgenden Ereignissen auf.
- Bei einem Würfelwurf fällt eine ungerade Zahl.
Ereignismenge:
- Beim Roulett wird kein schwarzes und kein rotes Feld getroffen.
Ereignismenge: (Die Null ist ein grünes Feld.)
- Alle möglichen Geburtstage im Monat Februar für die gilt, dass sie nach dem 29.2. stattfinden.
Ereignismenge:
- Aus einem Skatspiel (32 Karten) wird entweder eine Herz-Karte gezogen oder ein Ass.
Ereignismenge:
Aufgabe 3
Formuliere zu den folgenden zu einem Würfelwurf gehörenden Ereignismengen passende Ereignisse.
Es wird eine Zahl gewürfelt, die kleiner ist als 4.
Es wird eine gerade Zahl gewürfelt.
Die Zahl Eins wird gewürfelt.
Es wird eine Zahl gewürfelt, die größer oder gleich 5 ist.
Wahrscheinlichkeit eines Ereignisses
Die Wahrscheinlichkeit dafür, dass bei einem Zufallsexperiment ein bestimmtes Ereignis eintritt, wird mit einer Zahl zwischen 0 und 1 beschrieben.
Dabei bedeutet eine Wahrscheinlichkeit von 0, dass das Ereignis sicher nicht eintreten kann. Es ist ein unmögliches Ereignis [z.B. mit einem normalen Spielwürfel eine 8 würfeln]. Bei einer Wahrscheinlichkeit von 1 wiederum trifft das Ereignis sicher ein [z.B. mit einem normalen Spielwürfel eine 1, 2, 3, 4 ,5 oder 6 würfeln]. Das bezeichnet man als sicheres Ereignis.
Das lateinische Wort für Wahrscheinlichkeit ist probabilitas. Das englische Wort ist probability. Daher benutzt man in der Mathematik ein P. Wenn man schreibt, dann steht da kurz und knapp der Ausdruck “die Wahrscheinlichkeit des Ereignisses”.
Als Beispiel muss mal wieder der Münzwurf herhalten:
Schreibweise:
Sprich: “Die Wahrscheinlichkeit dafür, dass das Ereignis”Kopf" eintritt ist 0,5 oder 50%."
Was heißt das nun: Wirft man die Münze beispielsweise 100 Mal, so kann man etwa 50-Mal “Kopf” erwarten.
Zur Veranschaulichung von Wahrscheinlichkeiten kann man sich folgenden Maßstab vorstellen:
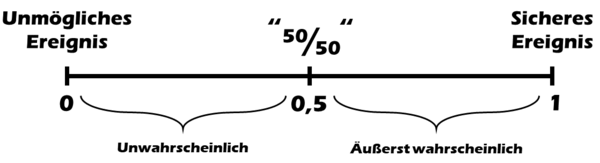
Hier sind einige Ereignisse auf diesem Maßstab eingeordnet:
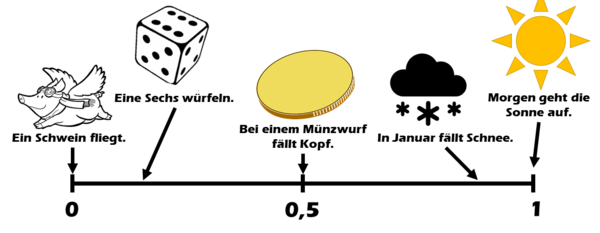
Beispiele:
:
Die Wahrscheinlichkeit eine Eins zu würfeln ist . Das heißt, würfelt man 100 Mal, kann man etwa 17 Mal eine Eins erwarten.
:
Eine Regenwahrscheinlichkeit von 30% bedeutet, dass man erwarten kann, dass es an 30 von 100 vergleichbaren Tagen, die alle eine Regenwahrscheinlichkeit von 30% haben, regnet.
Aufgabe 1
Was bedeuten die folgenden mathematischen Ausdrücke? Schreibe als Satz.
Die Wahrscheinlichkeit mit zwei Würfeln die Augensumme 12 zu würfeln ist . Das heißt, würfelt man 100 Mal mit zwei Würfeln gleichzeitig und ermittelt jedesmal die Augensumme, kann man etwa dreimal die Augensumme 12 erwarten.
Die Wahrscheinlichkeit blind eine gelbe Murmel aus der Hosentasche zu ziehen ist . Das heißt, zieht man 100 Mal eine Murmel aus der Hosentasche (und steckt sie danach immer wieder zurück!), kann man erwarten, dass man etwa 25 Mal eine gelbe Murmel erwischt.
Die Wahrscheinlichkeit blind ein h zu tippen ist . Das heißt, tippt man 100 Mal blind auf die Tastatur, kann man erwarten, dass man etwa einmal ein h erwischt hat.
Aufgabe 2
Schreibe die Sätze kurz und knapp als mathematischen Ausdruck.
- Die Wahrscheinlichkeit dafür, dass Nepomuk eine Antwort auf eine Frage weiß, ist 64%. Stellt man ihm also 100 vergleichbare Fragen, so kann man erwarten, dass er 64 von diesen Fragen beantworten kann.
- Die Wahrscheinlichkeit dafür, dass ein Marmeladenbrot auf der Marmeladenseite landet, ist 87%. Schmeißt man also das Marmeladenbrot 100 Mal vom Tisch, kann man erwarten, dass es 87 Mal auf der Marmeladenseite landet. Leider ist dann keine Marmelade mehr auf der Marmeladenseite.
Wie bestimmt man Wahrscheinlichkeiten?
Um nun die Wahrscheinlichkeiten von Ereignissen bei einem Zufallsexperiment zu bestimmen, gibt es verschiedene Strategien. Zwei habt ihr bereits kennengelernt. Die sollen hier noch einmal wiederholt werden.
Die erste Strategie
Man wiederholt das Zufallsexperiment häufig, um so die Wahrscheinlichkeit der verschiedenen möglichen Ausgänge schätzen zu können. Bei genügend großer Anzahl von Wiederholungen des Zufallsexperiments nähern sich die relativen Häufigkeiten der Ereignisse den theoretischen Wahrscheinlichkeiten dieser Ereignisse an. Dieser Zusammenhang wird als empirisches Gesetz der großen Zahlen bezeichnet.
Die zweite Strategie
Es gibt auch Zufallsexperimente, bei denen man sich die Wahrscheinlichkeiten der einzelnen Ergebnisse durch theoretische Überlegungen herleiten kann. Die wichtigsten Vertreter dieser Zufallsexperimente sind die Laplace-Experimente, bei denen alle Elementarergebnisse gleich wahrscheinlich sind.
Das empirische Gesetz der großen Zahlen
Wird ein Zufallsexperiment sehr oft durchgeführt, so stabilisieren sich die relativen Häufigkeiten eines Ergebnisses um einen festen Wert. Dieser Wert kann dann als Schätzwert für die Wahrscheinlichkeit des Ergebnisses verwendet werden.
Die Frage danach, wie viele Wiederholungen des Zufallsexperiments denn nun genug sind, kann dabei leider nicht eindeutig beantwortet werden. Die Antwort bleibt vage: VIELE!
Übrigens: Das Gesetz der großen Zahlen sagt nichts darüber aus, wie die absoluten Verteilungen einer Zufallsversuchsreihe aussehen muss. Das heißt, nur weil man bisher sehr wenig 6-en gewürfelt hat, müssen jetzt nicht viele 6-en fallen, um “den Rückstand auszugleichen”…
Aufgabe 1
Wirf das Schwein!
- Setze die Anzahl der Würfe auf 10. Wiederhole die Wurfserie ein paar Mal und beobachte die Ergebnisse (auch die relativen Häufigkeiten). Was stellst du fest?
Die relativen Häufigkeiten schwanken bzw. ändern sich sehr stark: Mal landet das Schwein in 100% der Fällen auf der Seite und nie in einer andere Position, mal landet es nur in 20% der Fälle auf der Seite…
- Setze die Anzahl der Würfe auf 100. Wiederhole die Wurfserie ein paar Mal und beobachte die Ergebnisse (auch die relativen Häufigkeiten). Was stellst du fest?
Die relativen Häufigkeiten schwanken bzw. ändern sich noch stark, aber nicht mehr so extrem wie in Teilaufgabe a). Es kann aber durchaus sein, dass beispielsweise keine Landung auf der Schnauze, auf der Backe oder im Stehen vorgekommen ist.
- Setze die Anzahl der Würfe auf 10000. Wiederhole die Wurfserie ein paar Mal und beobachte die Ergebnisse (auch die relativen Häufigkeiten). Was stellst du fest?
Die relativen Häufigkeiten ändern sich von Wurfserie zu Wurfserie kaum oder gar nicht mehr. Die so erhaltenen relativen Häufigkeiten können nun als Wahrscheinlichkeiten für die verschiedenen Landepositionen angenommen werden. Auf diese Weise erhält man folgende Wahrscheinlichkeiten für die verschiedenen Landepositionen:
Aufgabe 2
Drehe das Glücksrad!
- Drehe das Glücksrad (“Rad drehen”) mindestens 200 Mal. Beobachte dabei, was sich in der Tabelle und was sich im Diagramm ändert. Führe drei Serien durch.
Anfangs schwanken die relativen Häufigkeiten stark. Je öfter man das Glücksrad gedreht hat, desto stabiler bleiben die relativen Häufigkeiten.
Diese Schwankungen werden auch im Diagramm deutlich. Zunächst springen die Farbpunkte noch wild herum. Mit zunehmender Wiederholung des Experimentes nähern sie sich aber immer mehr den Linien in der gleichen Farbe an.
So könnte das Bild aussehen, wenn man das Glücksrad 1000 mal gedreht hat.
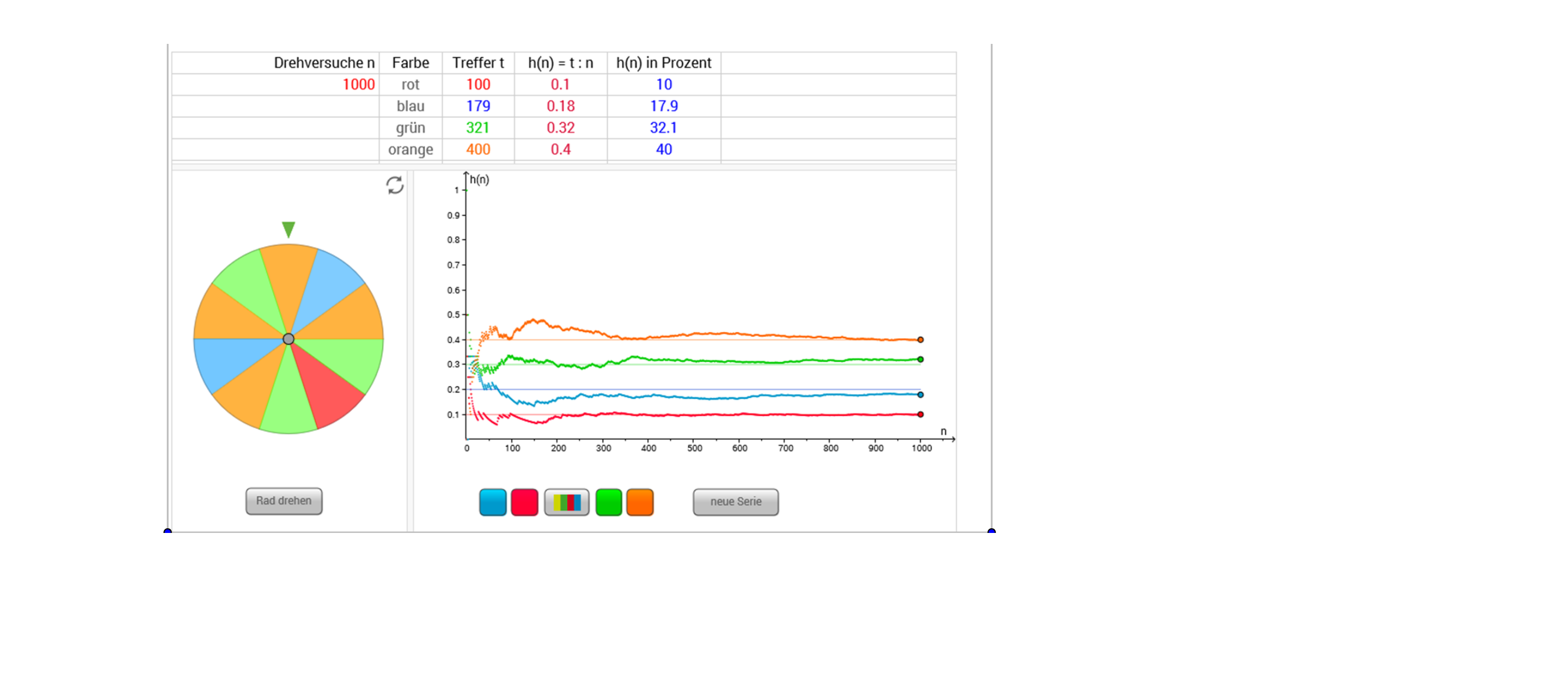
- Beschreibe das Experiment in eigenen Worten.
Man dreht ein Glücksrad, das 10 gleich große Sektoren hat. Einer davon ist rot, zwei sind blau, drei sind grün und vier Sektoren sind orange.
Nach jeder Umdrehung wird in einer Tabelle der Treffer mitprotokolliert. Bleibt das Glücksrad also beispielsweise bei einem grünen Sektor stehen, so wird die Trefferanzahl bei der Farbe grün um 1 erhöht.
Gleichzeitig werden alle relativen Häufigkeiten aktualisiert. Gab es bisher dreimal die Farbe blau und einmal orange, verändern sich die relativen Häufigkeiten bei einem ersten Treffer für grün wie folgt:
blau: von auf
orange: von auf
grün: von auf
rot bleibt bei
Diese relativen Häufigkeiten werden nun zusätzlich in einem Diagramm festgehalten. Nach jeder Drehung des Glücksrades werden die aktualisierten relativen Häufigkeiten als farbige Punkte in das Diagramm gezeichnet.
Als Orientierungshilfe dienen farbige Striche in dem Diagramm. Sie repräsentieren die theoretisch erwartbaren Wahrscheinlichkeiten: Drehen eines Glücksrades ist ein Laplace-Experiment, denn alle Sektoren sind gleich wahrscheinlich. Für die Farben gilt damit: Rot hat eine Wahrscheinlichkeit von (ein Sektor ist rot), Blau hat eine Wahrscheinlichkeit von (zwei Sektoren sind blau), Grün hat eine Wahrscheinlichkeit von (drei Sektoren sind grün) und Orange hat eine Wahrscheinlichkeit von (vier Sektoren sind orange).
Je öfter man das Experiment durchführt, desto mehr nähern sich die Punkt für Punkt entstandenen farbigen Linien den Hilfslinien in derselben Farbe an.
Aufgabe 3
Hans arbeitet als Kontrolleur für die KVB. In letzter Zeit hat er 1235 zufällig ausgewählte Personen kontrolliert und dabei 87 Schwarzfahrer:innen entdeckt.
- Wie wahrscheinlich ist es, dass die nächste Person, die er kontrolliert, keinen Fahrschein hat?
Hans hat das Zufallsexperiment der Fahrscheinkontrolle 1235 durchgeführt. Das ist ja schon ziemlich häufig. Dabei kam 87-mal das Ergebnis “Schwarzfahrer:in” heraus. Mit dem Gesetz der großen Zahlen können wir die realtive Häufigkeit nun als Wahrscheinlichkeit annehmen, also:
Die Wahrscheinlichkeit, dass die nächste Person, die er kontrolliert, keinen Fahrschein hat ist also 7%.
- Mit wieviel Verlust muss die KVB jährlich rechnen, wenn sie monatlich 27.000.000 Fahrgäste transportiert und ein Fahrschein 3€ kostet?
Die KVB transportiert jährlich Fahrgäste.
Wenn ein Fahrgast mit einer Wahrscheinlichkeit von 7% ein:e Schwarzfahrer:in ist, dann können wir also von Schwarzfahrer:innen jährlich ausgehen.
Damit ergibt sich ein Verlust von pro Jahr.
Aufgabe 4
Frau D. hat einen Würfel 125 Mal geworfen, ihre Ergebnisse protokolliert und folgende Häufigkeitstabelle erstellt:
| Augenzahl | 1 | 2 | 3 |
|---|---|---|---|
| Häufigkeit |
Leider hat sie vergessen, welchen Würfel sie verwendet hat. Sie weiß nur noch, dass eines der drei folgenden Würfelnetze zu dem verwendeten Würfel passen muss.
A
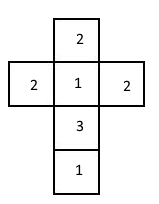
B
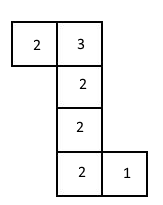
C

Welchen Würfel hat sie wahrscheinlich verwendet? Begründe deine Antwort.
Mit Hilfe der angegebenen Häufigkeiten kann man die relativen Häufigkeiten der Würfelergebnisse bestimmen. Diese nutzt man nun als Hinweis auf die tatsächliche Wahrscheinlichkeit eine bestimmte Augenzahl zu würfeln.
Für die Eins gilt:
Für die Zwei gilt:
Für die Drei gilt:
Betrachtet man nun die Würfelnetze, kann man feststellen, dass bei den Würfelnetzen 1 und 3 die Augenzahl zwei genau die Hälfte der Seiten des Würfels einnimmt. Würfelt man 125 mal, kann man die Zwei zwischen 60 und 70 mal erwarten (etwa 50% der Würfelergebnisse). Das ist hier der Fall. In 69 von 125 Fällen wurde eine Zwei gewürfelt - oder in Prozent ausgedrückt: in 55,2% der Fällen.
Da außerdem mehr Einsen als Dreien gefallen sind, ist es wahrscheinlich, dass die Eins auf mehr Würfelseiten vorkommt als die Drei. Das ist beim 1. Würfelnetz der Fall.
Damit kann man schließen, dass wahrscheinlich ein Würfel mit dem ersten Würfelnetz verwendet wurde. Dies ist aber nur wahrscheinlich der verwendete Würfeln,
denn die relativen Häufigkeiten können bei geringer Anzahl von Versuchsdurchführungen von der theoretischen Wahrscheinlichkeit (durchaus auch weit!) abweichen. Daher könnte auch einer der beiden anderen Würfel verwendet worden sein - sie sind nur unwahrscheinlichere Kandidaten.
Aufgabe 5
Im Jahr 2017 gab es 136,3 Mio. zahlende Nutzer von Musik-Streamingdiensten. Dabei verteilen sich die Nutzer auf folgende Anbieter:
| Spotify | Apple Music | Amazon Music | Andere |
|---|---|---|---|
Auf der Straße werden nun zufällig Passanten angesprochen. Wenn sie zahlende Nutzer von einem Streamingdienst sind, sollen sie befragt werden. Wie wahrscheinlich ist es, dass ein auf diese Weise zufällig ausgewählter Nutzer eines Streamingdienstes…
- … Kunde von Amazon Music ist?
Mit einer Wahrscheinlichkeit von ca. 12% ist der Nutzer ein Kunde von Amazon Music.
- … nicht Kunde von Apple Music ist?
Hier wird gefragt, wie wahrscheinlich es ist, dass der Nutzer NICHT Kunde von Apple Music ist. Hierfür muss man die Wahrscheinlichkeit berechnen, dass er Kunde von einem der anderen Dienste ist. Dazu addiert man die Kundenzahlen aller Streamingdienste, die nicht Appel Music sind:
54520000 (Spotify) + 16356000 (Amazon Music) + 39527000 (Andere) = 110403000
Damit ergibt sich für die Wahrscheinlichkeit, dass die befragte Person bei einem anderen Streamingdienst ist:
Mit einer Wahrscheinlichkeit von ca. 81% ist der Nutzer KEIN Kunde von Apple Music.
- … Kunde von Spotify oder einem anderen Dienst (Andere) ist?
Hierfür addiert man die Kundenzahlen von Spotify und Andere:
54520000 (Spotify) + 39527000 (Andere) = 94047000
Damit ergibt sich für die Wahrscheinlichkeit, dass die befragte Person Kunde bei Spotify oder einem anderen Streamingdienst ist
Mit einer Wahrscheinlichkeit von ca. 69% ist der Nutzer Kunde bei Spotify oder einem anderen Streamingdienst.
Laplace-Experimente und ihre Wahrscheinlichkeiten
Ein Zufallsexperiment, bei dem alle endlich vielen Elementarergebnisse die gleiche Wahrscheinlichkeit haben, heißt Laplace-Experiment. Sind n Ergebnisse möglich, so ist die Wahrscheinlichkeit jedes einzelnen Ergebnisses .
Beispiele für Laplace-Experimente sind würfeln (jede Augenzahl hat die gleiche Wahrscheinlichkeit ) oder auch eine Münze werfen (die möglichen Ausgänge “Kopf” und “Zahl” haben beide die Wahrscheinlichkeit ).
Bei einem Laplace-Experiment hat ein Ereignis die Wahrscheinlichkeit:
Die Wahrscheinlichkeit gibt hier also an, welche relative Häufigkeit eines Ergebnisses bei sehr vielen Wiederholungen erwartbar ist.
Was heißt das?
Stelle dir vor du würfelst 100-Mal mit einem fairen Würfel. Dann kannst du also erwarten, 17 Mal eine Zwei zu würfeln.
Beispiel
Betrachte das folgende Zufallsexperiment:

Man zieht eine Kugel aus der Urne. Da jede Kugel gleich groß ist, zieht man jede Kugel mit der gleichen Wahrscheinlichkeit. Es handelt sich also um ein Laplace-Experiment.
Wie wahrscheinlich ist es nun die Farbe grün zu ziehen?
, da eine der vier Kugeln grün ist.
Entsprechend gilt für die Wahrscheinlichkeit eine blaue Kugel zu ziehen:
, da drei der vier Kugeln blau sind.
Wie wahrscheinlich ist es die Zahl Zwei zu ziehen?
, da zwei der vier Kugeln mit einer Zwei beschriftet sind.
Aufgabe 1
In einer Urne befinden sich 20 Kugeln, die mit den Zahlen von 1 bis 20 beschriftet sind. Fatu zieht eine Kugel. Mit welcher Wahrscheinlichkeit …
- … zieht sie die Kugel mit der Zahl 12?
Es gibt genau eine Kugel mit der Zahl 12: . Die Wahrscheinlichkeit, diese eine Kugel zu ziehen, ist:
- … zieht sie eine Kugel mit einer durch 3 teilbaren Zahl?
Es gibt 6 Kugeln, die mit einer durch 3 teilbaren Zahl beschriftet sind, die Kugeln mit der Aufschrift 3, 6, 9, 12, 15 oder 18: . Die Wahrscheinlichkeit, eine dieser Kugeln zu ziehen, ist:
- … zieht sie eine Kugel mit einer Zahl, die größer als 11 ist?
Es gibt 9 Kugeln, die mit einer Zahl größer 11 beschriftet sind, die Kugel mit der Aufschrift 12, 13, 14, 15, 16, 17, 18, 19 oder 20: . Die Wahrscheinlichkeit, eine dieser Kugeln zu ziehen, ist:
- … zieht sie eine Kugel mit einer Quadratzahl?
Es gibt 4 Kugeln, die mit einer Quadratzahl beschriftet sind, die Kugeln mit der Aufschrift 1, 4, 9 oder 16: . Die Wahrscheinlichkeit, eine dieser Kugeln zu ziehen, ist:
Aufgabe 2
Der Teufel schlägt dir ein kurzes Würfelspiel vor. Du darfst dich dabei für eine Gewinnregel entscheiden. Du würfelst mit einem normalen Spielwürfel und gewinnst …
… bei einer geraden Zahl.
… bei einer ungeraden Zahl.
… bei einer Zahl kleiner 5.
… bei einer Zahl größer 5.
- Für welche Regel solltest du dich entscheiden? (Hier geht’s um deine Seele!!)
Am besten entscheidest du dich dafür, bei einer Zahl kleiner 5 zu gewinnen, denn:
Bei einem Würfelwurf gibt es sechs mögliche Ergebnisse () und zum Ereignis “eine Zahl kleiner 5 würfeln” gehören vier günstige Ergebnisse ().
Die Wahrscheinlichkeit “eine Zahl kleiner 5” zu würfeln ist also:
In diesem Fall gewinnt man also mit einer Wahrscheinlichkeit von 67%.
- Berechne für jeden der obigen Fälle die Gewinnwahrscheinlichkeit.
Du würfelst mit einem normalen Spielwürfel und gewinnst bei einer geraden Zahl:
Bei einem Würfelwurf gibt es sechs mögliche Ergebnisse () und zum Ereignis “eine gerade Zahl würfeln” gehören drei günstige Ergebnisse ().
Die Wahrscheinlichkeit “eine gerade Zahl” zu würfeln ist also:
In diesem Fall gewinnt man also mit einer Wahrscheinlichkeit von 50%.
Du würfelst mit einem normalen Spielwürfel und gewinnst bei einer ungeraden Zahl:
Bei einem Würfelwurf gibt es sechs mögliche Ergebnisse () und zum Ereignis “eine ungerade Zahl würfeln” gehören drei günstige Ergebnisse ().
Die Wahrscheinlichkeit “eine ungerade Zahl” zu würfeln ist also:
In diesem Fall gewinnt man also mit einer Wahrscheinlichkeit von 50%.
Du würfelst mit einem normalen Spielwürfel und gewinnst Zahl größer 5:
Bei einem Würfelwurf gibt es sechs mögliche Ergebnisse () und zum Ereignis “eine Zahl größer 5 würfeln” gehört ein günstiges Ergebnis ().
Die Wahrscheinlichkeit “eine Zahl größer 5” zu würfeln ist also:
In diesem Fall gewinnt man also mit einer Wahrscheinlichkeit von 16,7%.
Aufgabe 3
Ein Kartenspiel hat 32 Karten mit den Farben: Herz, Karo, Pik und Kreuz. In jeder Farbe gibt es jeweils die Karten 7, 8, 9, 10, Bube, Dame, König, Ass.
Wie hoch ist die Wahrscheinlichkeit für folgende Ereignisse:
- Es wird eine Karte der Farbe Karo gezogen.
In dem Kartendeck gibt es insgesamt 32 Karten, von denen 8 Karten die Farbe Karo haben. Daher gilt:
Mit einer Wahrscheinlichkeit von 25% wird eine Karokarte gezogen.
- Es wird eine Dame gezogen.
In dem Kartendeck gibt es vier Damen. Daher gilt:
Mit einer Wahrscheinlichkeit von 12,5% wird eine Dame gezogen.
- Es wird keine 10 gezogen.
In dem Kartendeck gibt es vier Karten mit einer 10. Damit gibt es 28 andere Karten: also 28 Karten, auf denen keine 10 steht. Daher gilt:
Mit einer Wahrscheinlichkeit von 87,5% wird keine 10 gezogen.
Aufgabe 4
Hier steht eine Urne, die noch keine Kugeln enthält.
Befülle die Urne jeweils so, dass die geforderten Wahrscheinlichkeiten eintreten. Die Grundmenge der Kugeln darfst du dabei frei wählen.
- Die Wahrscheinlichkeit eine blaue Kugel zu ziehen ist 25%.
Das ist z.B. dann der Fall, wenn es eine blaue Kugel und drei anders gefärbte (beispielsweise rote) Kugeln gibt, da dann gilt.
Natürlich wäre aber auch eine Befüllung mit zwei blauen und 6 roten Kugeln möglich. Oder auch 3 blaue, 3 gelbe, 3 rote und 3 grüne Kugeln….
- Die Wahrscheinlichkeit eine rote Kugel zu ziehen ist 10%.
Das ist z.B. dann der Fall, wenn es eine rote Kugeln und neun anders gefärbte (beispielsweise gelbe) Kugeln gibt, da dann gilt.
Natürlich wäre aber auch eine Befüllung mit zehn roten und 90 grünen Kugeln möglich. Oder auch mit 5 roten, 5 gelben, 20 grüne und 20 blauen Kugeln….
- Die Wahrscheinlichkeit eine grüne Kugel zu ziehen ist 15%.
Das ist z.B. dann der Fall, wenn es drei grüne Kugeln und 17 anders gefärbte (beispielsweise blaue) Kugeln gibt, da dann gilt.
Natürlich wäre aber auch eine Befüllung mit 15 grünen und 85 blauen Kugeln möglich. Oder auch mit 6 grünen und 12 gelben, 11 blauen und 11 roten Kugeln…
- Die Wahrscheinlichkeit eine gelbe Kugel zu ziehen ist 50%.
Das ist z.B. dann der Fall, wenn es eine gelbe Kugel und eine anders gefärbte (beispielsweise schwarze) Kugel gibt, da dann gilt.
Natürlich wäre aber auch eine Befüllung mit 5 gelben und 5 schwarzen Kugeln möglich. Oder auch mit 12 gelben und 4 grünen, 4 blauen und 4 roten Kugeln…
- Die Wahrscheinlichkeiten aus a), b), c) und d) sollen gleichzeitig eintreten.
Das ist z.B. dann der Fall, wenn es zwei rote, drei grüne, fünf blaue und zehn gelbe Kugeln gibt. Oder natürlich auch, wenn es 25 blaue, 10 rote, 15 grüne und 50 Kugeln gibt.
Wie löst man diese Aufgabe?
Am besten macht man sich zunächst Gedanken darüber, wie viele Kugeln insgesamt in der Urne sein müssen.
Da die Summe der vorgegebenen Prozentzahlen in diesem Fall 100% ergibt, kann man einfach die Prozentzahl ohne das Prozentzeichen verwenden und hat dann insgesamt 100 Kugeln.
Sollte die Summe der vorgegebenen Prozentzahlen nicht 100 ergeben muss man sie entweder durch eine nicht vorgegebene Farbe auf 100% ergänzen oder man multipliziert die vorgegebenen Prozentzahlen geschickt mit dem gleichen Faktor, so dass ihre Summe anschließend 100% ergibt.
Möchte man weniger als 100 Kugeln verwenden, kann man versuchen alle als Prozentzahlen gegebenen Anteile mit derselben Zahl zu kürzen. In unserem Beispiel geht das: Man kann die Porzentangaben , , und alle mit 5 kürzen und erhält dann , , und . Insgesamt benötigt man also 20 Kugeln. Die Zahl die jeweils im Zähler steht, gibt die Anzahl der von der jeweiligen Farbe benötigten Kugeln an.